

 |
 |
Krista Francis and Michele Jacobsen
University of Calgary, Canada
Math is often taught poorly emphasizing rote, procedural methods rather than creativity and problem solving. Alberta Education developed a new mathematics curriculum to transform mathematics teaching to inquiry driven methods. This revised curriculum provides a new vision for mathematics and creates opportunities and requirements for professional learning by teachers. Conventional offsite, after school, or weekend professional development is typically “sit and listen, maybe try on Monday”. Professional development that is embedded, responsive, and personalized is known to be more effective at changing teaching practice. Alberta teachers are geographically dispersed making online professional learning a desirable alternative to on-site workshops. As access to and use of the Internet gains momentum in schools across the country, opportunities for collaborative, online professional development become more viable. The online professional development in this hermeneutic study maps on to the new vision promoted in Alberta’s math curriculum, and addresses the challenge of a distributed teacher population. Thirteen geographically dispersed participants, including 10 teachers, a PhD mathematician, and two mathematics education specialists, collaborated in an online professional learning community to build knowledge for teaching mathematics. This paper describes and interprets the shared experiences of learners within an online, synchronous learning community that focused on discipline rich, focused inquiry with mathematics. Findings show that the nature and quality of the mathematics task impacted the quality and nature of the online interaction. Mathematics problems that incorporated easily drawn symbols and minimal text worked best in the online collaborative space. Members of this learning community discovered how to assert their identity in the online environment.
Keywords: K-6 education; teacher professional development; mathematical problem-solving; synchronous online learning environments; professional learning communities
Math is often taught poorly with an emphasis on procedural rote methods rather than designs for creative thinking; often, students hate math and teachers are not well prepared to teach math effectively (Ball, Thames, & Phelps, 2008; Friesen, 2008; Jacobs et al., 2006; Schoendfeld, 2009; Stigler & Hiebert, 2009). The revised Alberta curriculum was developed to purposefully shift mathematics teaching from procedural mathematical tasks to designs that engage learners in solving complex non-routine problems (Alberta Education, 2007). The new vision for mathematics teaching created a need for professional learning opportunities for teachers. Math teachers are distributed across the province, which can make it difficult to provide high quality professional learning for all math teachers. Online professional learning is a viable alternative to on-site workshops. With the advent of this new philosophy and research informed approach to teaching mathematics, teachers in schools are called upon to grapple with the following questions as they redesign their instructional designs and teaching practices: What are these mathematical processes? Why are these processes important? And, how are these mathematical processes supported and developed in the classroom?
It is well known that to successfully implement new curricula, teachers need professional learning opportunities and ongoing support to make the needed changes to their pedagogical practices (Darling-Hammond & Bransford, 2007; Fernandez & Yoshida, 2004; Jacobsen, 2006; Stigler & Hiebert, 1999).
Professional development is often offsite, after school, and on weekends. Geographic and temporal limitations often prevent suburban and rural teachers from being able to attend meaningful and transformative, face-to-face professional development opportunities. In their seminal work on educational reform, Darling-Hammond and McLaughlin (1995) outlined the difficulty that many teachers face accessing quality professional development while attempting to transform their teaching. The quality of professional development is measured by the teachers’ success in developing pedagogical competencies and perspectives, which are reflected in new visions and approaches to practice, while unlearning the beliefs about students and methods of instruction that have dominated their professional lives to date.
Unfortunately, few occasions and little support for meaningful, transformative professional development exist in many teachers’ environments (Darling-Hammond & McLaughlin, 2011). Conventional professional development does not transform teaching. Teachers often have little or no choice in the type and timing of their professional development. Most professional development is pre-determined, “sit and listen, maybe try it on Monday” with a one size fits all approach. To be more effective, the professional development needs to be embedded in the classroom, responsive to the teachers’ needs and experience, tailored, and personalized. Online (delivered via the Internet) professional development is viewed as having potential for providing diverse and meaningful learning opportunities for teachers (Darling-Hammond & McLaughlin, 2011).
Bringing teachers together online for professional learning has been described using a number of terms including online teacher professional development (oTPD) (Dede, Ketelhut, Whitehouse, Breit, & McCloskey, 2009; Marrero, Woodruff, Schuster, & Riccio, 2010), professional learning communities (PLCs) (DuFour, DuFour, Eaker, & Many, 2010; Stoll & Louis, 2007), professional learning networks (PLNs) (Lieberman & Grolnick, 2005; Trust, 2012), in higher education, asynchronous learning networks (ALNs) (Hiltz, 1998; Rovai, 2002), and simply as online learning communities (Mackey & Evans, 2011).
Wenger, Trayner, and de Laat (2011) distinguish between a PLN and a CoP. They define a PLN as
the set of relationships, personal interactions, and connections among participants who have personal reasons to connect. It is viewed as a set of nodes and links with affordances for learning, such as information flows, helpful linkages, joint problem solving, and knowledge creation. (p. 9)
In contrast, a CoP requires “the development of a shared identity around a topic or set of challenges. It represents collective intention – however tacit and distributed – to steward a domain of knowledge and to sustain learning about it” (p. 9). The terms that best describe the nature of learning sponsored by the design of this study are online teacher professional development (oTPD) (Dede, et al., 2009).
Not all online professional development can be considered meaningful and effective. Dede, et al. (2009) noted a proliferation of large-scale online teacher professional development (oTPD) studies. In a meta-analysis, the research team categorized 40 oTPD research studies into four themes: program design, program effectiveness, program technical design, and learner interactions. Most of the oTPD program and research initiatives centered on “program design and effectiveness within a community-of-practice theoretical framework” (p. 13). Their analysis suggests that market driven evaluative research is preferred over research that “informs design and extends our understanding of models that affect teacher learning and behavioural change” (p.13). Despite millions of dollars being spent, and extensive research (Dede, et al., 2009), the professional development that most teachers experience is fragmented, superficial, and ineffective (Borko, 2004).
Many of the online professional learning opportunities for teachers are large scale. For example, large PLNs include Classroom 2.0 with more than 61,000 members, Edmundo with 6.5 million users, and The Educator’s PLN with 11,000 members (Trust, 2012). The Math Forum (http://mathforum.org/) offers teacher resources, online workshops, and online forums and lists 800,000 visits per month (Renninger & Shumar, 2002).
Dede’s (2004a, 2004b) research described six requirements for professional development to improve education: (1) a shift from rote methods for high stakes testing to 21st century knowledge and skills, (2) a focus on transformational strategies, (3) a shift from “make and take” professional development to ongoing teacher driven professional development, (4) a shift from passive professional development to active teacher engagement through collaborative learning communities of researchers and practitioners; (5) synchronous distributed learning opportunities that maximize available media tools, and (6) distributed learning opportunities, which are powerful mechanisms for knowledge diffusion when they exemplify practice and impart the innovations reinforcing systematic change. Collaborative online professional development was found to be desired by teachers (Marrero et al., 2010) and to expand teachers’ knowledge, skills, and ideas (Glazer, Hannafin, Polly, & Rich, 2009)
Almost all Canadian schools are now connected to the Internet. In a pan-Canadian survey, Plante and Beattie (2004) found that schools averaged one computer per five students, and that close to 100% of schools were connected. Statistics Canada (2010) data indicates that in 2009, 80% of Canadians aged 16 and older, or 21.7 million people, used the Internet for personal reasons, which indicates an increase of 7% from 2007 when the survey was last conducted. In Alberta, SuperNet is a government initiative that provides affordable high-speed network connectivity and internet access to all schools, post-secondary institutions, libraries, hospitals, provincial government buildings, and regional health authorities in the province, which amounts to connecting over 4,700 sites (Alberta Education, 2012).
As access to and use of the Internet proliferates in schools across the country, more opportunities for online, collaborative professional development of teachers are being designed. What this means is that every Alberta teacher has access to the Internet at school, and can take advantage of online professional development opportunities and professional networks. Examples of online professional development include Alberta Professional Development (http://www.albertapd.ca/), which offers webinar courses and recordings of previous webinars; the Southern Alberta Professional Development Consortium’s Online Math Symposium (http://www.sapdc.ca/ ) with one day of online presentations; and the Alberta Regional Consortia (http://www.arpdc.ab.ca/), which provides access to online demonstration classes. While these programs provide access to learning opportunities to geographically dispersed teachers, they are not tailored, responsive, and personalized. In this study, our purpose is to describe the intent and formation of a professional learning community that is small, responsive, personally connected, embedded, situated, and meaningful to the participants to continually improve their teaching practices.
The pedagogic format for this study was borrowed from a face-to-face professional learning program developed at the Galileo Educational Network (GENA) called Lesson Study. The program was designed, in part, based on a Japanese form of professional learning where teachers collaboratively plan, implement, and revise teaching lessons (Fernandez & Yoshida, 2004; Moore, 1993). The positive impact of collaborative approaches to support teachers’ design of learning is well documented (Fernandez & Yoshida, 2004; Jacobsen, 2006; Preciado-Babb & Liljedahl, 2012; Stigler & Hiebert, 2009). The Lesson Study process provides ongoing professional development for teachers to create ideas and design artefacts to implement in class. The process of collaborative learning design has contributed to the transformation of rote procedural teaching practices to problem solving approaches in Japanese schools (Stigler & Hiebert, 2009). Additionally, students in Japan consistently demonstrate higher achievement results in international tests (Martin, Mullis, & Foy, 2008; Mullis, Martin, Gonzales, & Chrostowski, 2004).
At GENA’s monthly two-hour sessions of Lesson Study, teachers would gather from across Calgary to work on rich mathematical problems with mathematicians and mathematics educators. The goals for Lesson Study were for teachers to experience learning mathematics as learners themselves, and to design learning experiences for their students that cultivated imagination and creativity with mathematics. The key elements of GENA’s Lesson Study considered important to transforming teaching and learning included a) collaboration and professional dialogue amongst teachers, mathematicians, and mathematic experts to investigate and solve good mathematical tasks together; and b) the collaborative development of ideas and artefacts for implementing inquiry learning tasks in the classroom.
In this study, we describe what we learned as we transformed GENA’s Lesson Study into an online, professional learning format. In four synchronous sessions we sought insight into the following research questions:
An interpretive hermeneutic approach was chosen to re-establish a research connection to original human experience. Hermeneutics is about finding practical knowledge in the everyday experience (Smith, 1999). Few studies focus on what teachers and students are doing with new technologies and how they are adapting to complex circumstances in educational practices (Friesen, 2009); this study attempted to address the gap. Hermeneutics was chosen to inform the study for several reasons: (1) hermeneutics is consistent with an emergent approach to designing online learning environments (Friesen, 2009); (2) rich, descriptive, context-dependent knowledge is valuable for understanding human learning processes (Flyvbjerg, 2001); (3) the fecundity of the individual case is a powerful interpretive tool for understanding pedagogy (Jardine, 2006); (4) exploration and discovery is necessary for learning and understanding in a study (Van Manen, 1997); (5) hermeneutics permits a focus on mathematics and interactions with mathematics in accordance; and (6) hermeneutics situates the study in the lifeworld to facilitate understanding of lived experiences with mathematics online.
Thirteen participants joined the study. Lily, a PhD mathematician from British Columbia, assisted in developing each inquiry session. Lily1 had a rare combination of characteristics that were believed to be necessary for the study. Lily was interested in K-12 education, valued mathematical problem solving, and was comfortable with technology. Sharon, a PhD mathematics educator, and Ella, a mentor for teachers, provided expertise on teaching mathematics. Sharon and Ella both worked at GENA. An invitation to participate in the online mathematics professional learning community was sent to teachers who had participated in Galileo Network’s professional development in previous initiatives. Ten teachers from around Southern Alberta were selected from this convenience sample of volunteers. The participants were chosen because they had indicated their desire to continue with GENA’s professional development, and had an interest in exploring how to better teach mathematics. The teachers who were included in this study had experience teaching grades five to nine. One principal at one rural school, a former GENA professional development participant, invited six teachers to participate together. The other five teachers all held previous experience with GENA’s professional development and were from unique schools located in different geographic locations in Alberta.
Hermeneutics is an approach that enables the researcher to be responsive to the situation at hand. Several sources of data were collected for analysis and interpretation in this study. While the experiences of participants in the four Elluminate™ sessions were the primary source of data, the conversational interviews conducted at the beginning and the end of the study, asynchronous text discussions, emails, informal telephone and face-to-face conversations, and field notes also supplemented the analysis. Each of the four sessions was digitally recorded, preserving audio and visual images. In an iterative process of listening, observing, writing, and reading, the hermeneutic text was formed ( Friesen, 2009; van Manen, 1997).
This section describes the online learning experiences as they unfolded chronologically and the nature of participants’ learning experiences in the four Elluminate™ sessions. Due to a desire for succinctness, the following chronology summarizes rather than narrates the collective experience. Each event has two components: (1) A pre-session online meeting where Lily and Krista tested the mathematical problems, and (2) the online learning experiences with participants.
Prior to meeting with participants, Lily emailed mathematical problems for the first session in a black and white PDF image. Krista added colour images and formatted the problems into slides that could be uploaded for the session. Lily had never used Elluminate™ or any other computer-mediated learning environment before, so Krista and Lily conducted a trial in Elluminate™. Lily learned how to depress the microphone button to talk and experimented with the online toolset. Lily provided a photocopy of a coding problem which required deciphering shape coded integers in algebraic equations. I reproduced the problem in colour to make it more appealing. Within half-an-hour, Lily felt comfortable enough with the technology to help moderate the session. An email was sent to all participants with information about the upcoming session and directions for testing their systems.
Thus we shall never experience our relationship to the essence of technology so long as we merely conceive and push forward the technological, put up with it, or evade it. (Heidegger, 1977, p.4)
Unfortunately, the first online professional learning experience was a frustrating breakdown of communication. We encountered firewalls, non-functioning microphones, and issues with usernames and passwords. A group of teachers in rural Alberta and one teacher in Calgary found that they could not access Elluminate™. With much deliberation through phone calls and emails, we concluded that firewalls were preventing the connection. Many school divisions put up firewalls to block social networking sites (Clifford, Friesen, & Lock, 2004; Jones & Cuthrell, 2011): an institutional IT decision that excluded half of the invited participants from the session. Another participant had difficulty logging in; his user ID and password would not work. We were unable to alleviate this participant’s technical issues; he was unable to join the session.
Of the six of us that did connect, three microphones did not work, including the primary researcher’s microphone. The on-campus, faculty IT support person arrived late to the sessions and plummeted into a hotbed of technical issues. Jonassen (2004) describes a cognitive process that is required to solve trouble-shooting problems that begins with “identify the fault state and related symptoms” (p. 13) and continues through a linear series of diagnoses that ends with “repeating the process of generating and testing hypotheses until the fault is identified” (p. 14). The faculty IT support person was expected to help identify the audio problems and get participants connected.
Unfortunately, we found ourselves stuck in a troubleshooting feedback loop (see Figure 1). The faculty IT support person hypothesized that the microphones were faulty and asked me (and several others) to test the problem. Given the functionality of the mic in the pre-session, I was certain that it was not the problem. Each time that I did not test the hypothesis (i.e., try a different mic), the support person could not be sure that the hypothesis was incorrect and thus could not reject the hypothesis. Without being able to reject the hypothesis, a new hypothesis was not formulated.
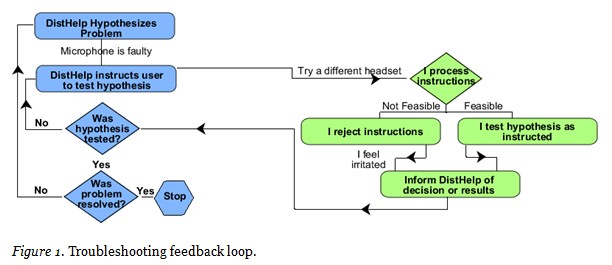
Held in a continual infinite loop, the issues were not resolved in this first session. After the session, we discovered how to configure the OSX system to the USB headsets.
While initial online experience with teachers enabled us to explore a math problem together, it felt like a technological nightmare. We questioned the impact of such technological issues on new instructors. Will new instructors who experience challenges with technology dismiss or discount the value of online spaces? What is the likelihood they will want to continue? Will they believe in the possibilities for meaningful and engaged learning in online courses? Will they “put up with it, or evade it” (Heidegger, 1977, p. 4)?
The problems we experienced offered insightful reminders that online educators cannot expect technology to work perfectly the first time. When embarking on any new synchronous collaboration, anticipate that the first session will offer a technology learning session for participants to get used to the tools. Anticipate firewall issues that require advanced technical support. Know who to contact beyond initial microphone testing and connection help.
Shortly after Session 1, one participant withdrew from the study. Considering our previous challenges from Session 1, we were grateful no one else withdrew. Again, Lily emailed math problems to the researcher for the session. Lily chose word problems with an Alice in Wonderland theme. Krista added static images to the word problems to make the problems more visually appealing on the whiteboard. In the pre-session, we worked the problems and were satisfied with their functionality.
I didn’t like doing school work….School was boring. And the school work I was learning was boring. Boring, boring, boring. (Clifford & Friesen, 2003, p. 92)
Prior to Session 2, firewalls were removed by the upper level IT in the school boards and we had all learned how to configure our audio microphone settings. During Session 2, the conversation among the participants seemed stifled. One participant chose to ignore the problem and was “away” for the entire session. Lily repeatedly called upon people to invite them to participate. As Lily tried to entice participants, she eventually demonstrated the solution to the problem.
|
Lily: |
2 times 1000 plus 0 times 100 plus 0 times 10 plus seven times one. Then that 2 times 1000 equals 2 times 999 plus 2 times 1. With modular arithmetic or remainder arithmetic, you do not need to worry about anything times 999. You can then use the trick to get rid of the two times 999. We only have 7 plus 2 equals 9 to deal with. 9 is divisible by 9 therefore 2007 is divisible by 9. If 2007 is divided by 9, the number of papers would have been 2007+1, and Alice is right. Does that make sense or am I talking to myself? |
|
Sandy: |
I am really sorry Lily, but my Grade 6 brain is not processing what you just explained to us. I can’t see on the whiteboard the times 100 work that you were doing, so I am really lost. |
|
Lily wrote on the board 2*1000=2*999 + 2*1 |
|
|
Lily: |
Can you see now? |
|
Sandy: |
Yes now it has come up. |
|
Samantha: |
Now that it is on the board I see that, but why specifically is it significant to this problem to be able to do that. |
|
Lily: |
The main idea is to use the distributive law to break this number’s powers of 10, into multiples of 9 plus 1. Like 999 plus 1 and 99 plus 1 and 9 plus 1. Once you tag on the place value of 2007 you have 2 times 1000, 0 times 100, 0 times 10 and 7*1. All that allows you to throw away the 999. Anything multiplied by 999 is still divisible by 9. We just have to look at the ones – the 2 times one plus the 7 times 1 |
|
Micky: |
I am seeing that now. Thanks Lily. |
In Figure 2 is a screen capture of the problem and Lily’s solution as it appeared in Elluminate.

Something was not quite right in Session 2. We observed that the nature of the mathematical problem seemed to adversely influence interaction in the online environment. The interaction could be characterized as instructor-student with very little student-student interaction (Moore, 1989, 2007). Upon reflection, we realized the problem text occupied the bulk of available whiteboard space, which reduced the space available for participant interaction (see Figure 2). With the available tools, we had difficulty typing and drawing numbers on the whiteboard screen. Forming letters and numbers with a mouse was difficult. Consequently, the problem was unsuitable for the chosen media. To borrow from Clifford and Friesen’s (2003) quote above, the session turned out to be boring.
On the one hand, Session 2 taught us how quickly technological problems can fade. The learning community experienced few problems with login and interaction. We also learned that filling the whiteboard space with the problem text limits the potential for student-student interaction. The experience in Session 2 taught us that a routine procedural problem stifles mathematical conversation and exploration.
For future sessions, we sought less routine calculation problems with fewer words to occupy less whiteboard space. Discrete mathematics is a loosely defined term that includes combinatorics, vertex-edge graphs, iteration, and recursions (DeBellis & Rosenstein, 2004). Goldin (2010) argues that discrete mathematics provides opportunities for interesting, non-routine problem solving and mathematical discovery. In an Elluminate™ planning session, Krista challenged Lily with a discrete mathematics problem called Jumping Chips (Lewis, 2002) that used the interactive features of the medium. This problem required participants to slide and jump chips to solve the problem. Instead of writing/typing numbers and equations, participants could move objects on the whiteboard. In response to this interactive experience, Lily excitedly exclaimed she had some ideas for problems.
This is mathematics we are talking about, the language in which, Galileo said, the Book of the World is written… For mathematics itself is the study of connections: how things ideally must and, in fact, do sort together – beyond, around, and within us. (Kaplan & Kaplan, 2007, p. 5)
The math problem for Session 3 employed minimal text and required participants to use drawing sticks on the whiteboard to explore solutions (see Figure 3).
When participants logged in for Session 3, they were encouraged to practice drawing sticks on the title page. Within a few minutes, the page was messily marked up with black sticks. As the board began to get messy, Lily piped in, “Could you please pick a colour and let me know who is drawing with that colour?” Soon we had a colour-coded key ascribing a name and colour identity to the sticks.
Lily’s toothpick problems drew upon the Roman numeral system and algebraic reasoning. As Lily began to explain the problem, Brice jumped onto the board with an incorrect solution. Brice moved the vertical line of the plus sign to form IIII as the answer: IX-V=IIII. Lily used Brice’s error as a chance for dialogue. Lily clarified, “Roman numeral systems do not use four sticks to write a four.”
A flurry of activity erupted as participants used the space to explore solutions. Micky rewrote the problem in red. Brice’s orange answer disappeared in a blink of an eye. Anonymous green lines appeared. Maggy texted that she tried, but was on the wrong track. An orange answer suddenly appeared. Once again, Brice solved the problem. Lily encouraged Brice to justify his solution strategy.
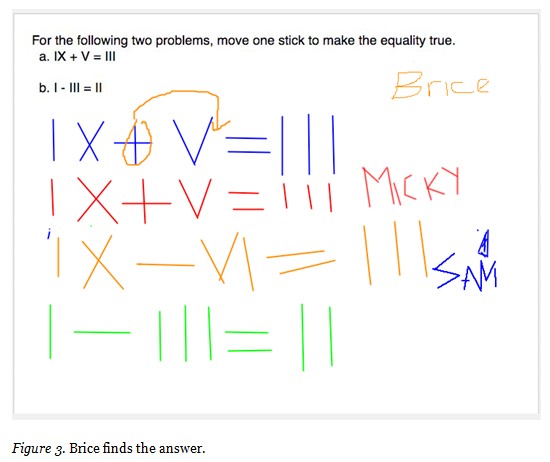
|
Lily: |
Brice got that. Wow! That was really fast. How did you do that? |
|
Brice: |
Once I figured out that we could just move the equation from addition to subtraction, I just looked at different combinations of numbers and operators. |
|
Lily: |
OK, thank you Brice. |
The polite stifled atmosphere dissipated into enthusiastic and unrestrained conversation about playing with and teaching mathematics. We talked about some of the emotional baggage teachers have surrounding mathematics: panic and being slow. While their subjective emotions about mathematics initially interfered with the participants’ willingness to play, it also exposed shared vulnerabilities that appeared to relax the group, a collective form of letting go. Lily and Sharon described the connections of mathematical creativity and competency. Everyone in the group contributed to the conversation and tried to solve the problem.
Session 3 was a turning point in the development of this online learning community. We had “move(d) from learning to use ICT to using ICT to learn” (Haughey, 2006, p. 2). For Session 3, Lily chose a non-routine problem which was entirely different from the procedural problems of Session 2. With minimal text, the problem suited the whiteboard. By requiring participants to draw sticks for creating solutions, the problem encouraged interaction with the tools. By choosing unique colours, we created online identities. The problem was non-routine and connected several mathematical concepts, including equivalence, number, and the history of the number system. The participants reported feeling comfortable risking mistakes in problem solving, trying creative solutions, and revealing their attitudes about mathematics. Collective conversations about our own learning needs and experiences with mathematics led us into deeper conversations about students’ learning and how to teach mathematics and design challenging tasks. The depth of mathematical conversation sponsored in the online environment demonstrated knowledge building and collaborative design in community.
In Session 3 we achieved the right combination of conditions to optimize online professional learning with mathematics. The technology faded and the mathematics conversations were amplified. The essential conditions included: 1) a complex non-routine mathematical problem for which easily drawn manipulatives facilitated the development of solution methods, 2) established identity of participants and trusting relations, 3) sufficient experience with the technological environment, and 4) adequate time to develop and cultivate our professional learning conversations and knowledge building interactions.
Lily brought Nim for our next session, a two-person game that requires the removal of chips to find a solution. In the test session, Krista mistakenly thought participants could easily draw circles on the whiteboard. The task turned out to be too cumbersome and the formulated circles were too uneven. Recalling the ease of drawing lines in Session 3, Lily suggested creating static images of the disks in rows. With a prepared template, uniformity and organization could be ensured. Also, a line drawn through the disc provided an easy removal of chips.
The chief forms of beauty are order and symmetry and definiteness, which the mathematical sciences demonstrate in a special degree. Aristotle
In every session, participants and the instructors were learning and adapting within the emergent online community. In Session 4, Lily engaged participants in the two-player game called Nim. Similar to the math problems in Session 3, this game demanded that participants play using the whiteboard tools. Lily encouraged participants to articulate their thoughts and strategies while playing with Nim. There was no lurking allowed in this session; everyone was called upon to play and contribute to the conversation.
We observed that as soon as the first problem slide appeared in Session 4, the group immediately started writing their names in their chosen color.

Brice and Sandy jumped in and immediately played the game. After Brice won, Lily suggested that Abby and Gerald play together. Abby made the first move, crossing off the left most chip. Gerald crossed off the middle chip. Abby crossed off the second chip. Gerald crossed off the last two chips, won the game, and exclaimed, “It looks like I won.” Lily replied, “Gerald, could you take off your last two crosses and Abby, could you remove your second stick. I would like to consider what was happening after the first two moves.”
The board was erased and Abby drew a line through the first circle again. Gerald drew his second line through the middle disc (see Figure 5 below).
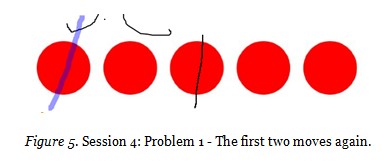
Lily interjected, “At this point can you see who can win? It is Abby’s turn. Suppose we give Abby more time to think. Would it be possible for Abby to win from here?” Abby crossed off the last circle in the row. Gerald was no longer able to win. Whichever circle he took, there would be one circle remaining. Lily probed, “a change of Abby’s second move meant she won. Why?” Gerald articulated that if the first person took the middle chip and then copied the moves of the second player, the first person would always win. Lily restated Gerald’s copying strategy as the mathematical principle of symmetry.
For the remainder of the session, participants explored whether the strategy of symmetry worked with other scenarios. Learners played with six chips, seven chips, and then two-dimensional versions. Lily shuffled everyone up, ensuring that everyone played and that everyone was able to utilize symmetry as a strategy.
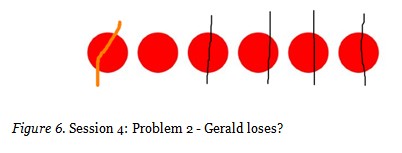
The next problem had six discs in row. When Gerald and Brice were playing together, lines were drawn and erased several times. Finally, the game was over when Gerald drew the two lines on the far right.
|
Lily: |
Hey how did that happen? Gerald how could you let Brice win? |
|
Gerald: |
Good question. I think we have a little rat over here. I think Brice is manipulating the colours and the lines here. |
Lily laughed appearing to enjoy Brice’s manipulation of identity. Brice had used deception of identity (different colored lines) which created a sense of playfulness.
We observed that the participants were collaborating to solve problems together. The Nim problems that Lily chose required two players. As the group observed two participants playing, we learned from the strategies they used. When we played in teams, we tested what we had learned from the observation. The other participants watched the new game and cheered on the “winner”. Jokes were made; laughter was heard; fun was had; and mathematics was learned.
The task of Nim turned out to be ideal for online mathematical learning and community conversation purposes. Drawing sticks was quite easy on the whiteboard. The game required participants to interact with each other using the whiteboard in order to play the game. As two participants played, the others could watch and learn, which demonstrates knowledge building in community and the emergence of community knowledge. Lily moderated by ensuring that everyone actively participated on the whiteboard – lurking was not allowed. She also encouraged participants to communicate their strategies, to think aloud, which made their strategies both visible and available as a narrative. Lily connected our informal vocabulary into mathematical terminology by reading back, or restating, the participants’ contributions using mathematical principles and language, which also contributed to the development of group knowledge.
This hermeneutic study sought to provide illustrations and insights into the interactive nature of collaboratively problem-solving with mathematics in an online professional learning community. An interpretive analysis of online learning experiences with mathematics across the four sessions yields key insights about (1) pedagogical design, 2) appropriate mathematical problems / tasks, and 3) sponsoring knowledge building and online collaboration with mathematics using technology.
The key finding from our research questions was the tremendous importance of the mathematical task. The nature of the mathematical task impacted (1) the use of the online technology, (2) the professional learning, and (3) the collaboration and mathematical problem solving. Our findings are directly relevant to the revised curriculum that requires teachers to design inquiry learning experiences in math for students. The type of learning that teachers experienced in the study was exemplary of the type of learning experiences that they are expected to design and support for their students.
Additionally, the hermeneutic study of teachers’ experiences was consistent with inquiry approaches to learning. Hermeneutics begins with understanding the lived experience and situating the historical, cultural, and literary context of the experience. Understanding deepens with more experiences along a hermeneutic circle or spiral (Gadamer, 1989; Heidegger, 1962). Each session traversed us further on the hermeneutic spiral deepening our understanding of how to create meaningful online mathematics teacher professional development. With inquiry, meaningful experiences deepen understanding of an issue, question, or problem. Hermeneutics was the appropriate approach to gain insight into an innovative approach to professional development. For an innovation, studying the lived experiences of the participants revealed deep insights into how to create meaningful online professional development for mathematics teachers.
The key contributions of this study are, first, the connection between the nature of the mathematical problem and promoting meaningful interactions using synchronous online technology, and, second, new insights about cultivating mathematical problem-solving conversations among educators to inform ongoing teaching and design of learning tasks.
From a technological perspective, mathematical problems that required minimal writing and more drawing appeared to work best in this online learning environment. Using the tools in Elluminate, participants could easily draw lines. In contrast, typing could easily run off the whiteboard, and writing text with the mouse was cumbersome. Also, problems with too much text minimized the amount of whiteboard space for collaborative interaction and participant voice. From a mathematical problem-solving perspective, routine, procedural, calculation problems lead to stifled, polite, and disengaged involvement and interaction amongst the participants. Conversely, multifaceted, non-routine, discrete problems fostered the most engaged and playful mathematical spaces for active learning, discovery, collaboration, and broad connecting conversations amongst educators in the online learning community.
Each session contributed to the graduated journey of learning for the participants in this online learning community. In each session, we asked participants to consider, “what was technology asking of us?” and “what was mathematics asking of us?” Session 1 was plagued with unresolved technical difficulties: firewall blockades, login trouble, and audio problems. The issues were entirely frustrating for all of the participants and impeded the community’s ability to communicate. Connecting synchronously was complicated and the entire group needed to learn how to overcome many unforeseen obstacles. However, the technological challenges in this first online learning experience were not repeated in subsequent sessions, and did yield some important group problem solving strategies and more familiarity with the technology.
In Session 2, Lily provided the participants with a routine calculation problem that was hidden within a lengthy text: a word problem. In terms of mathematics and mathematical conversations, we observed the conversation tended to be stifled and focused on the solution procedures for the problem in question, rather than the engaged, active interaction that was hoped for and expected. One participant chose to ignore the problem and was “away” for the entire session. The participants appeared to need Lily’s coercion and constant prompting to engage in mathematical conversations. Lily pointedly asked individual participants questions to draw them into conversations; however, we observed that no one volunteered or spontaneously jumped into the conversation – much like a conventional math class in school! A procedural mathematical task did not elicit a sense of collaborative problem solving. In terms of technology, typing text and numbers for the solution was difficult for participants given the available whiteboard tools. In retrospect, we realized that a graphics tablet and pen may have made the participant’s ability to write on the whiteboard easier. However, the expense of graphics tablets prevented our ability to use them for this study. A wordy procedural problem requiring text for the solution turned out to be an unsuitable problem for encouraging online collaborative problem solving in this session.
With the complex, non-routine problems that were presented in Sessions 3 and 4, the online community participants were able to make connections into the broader ideas of mathematics. Using easily drawn lines to form Roman numerals, Session 3 connected the learning community to the concept of equivalence, the concept of number, and the history of the number system. Collectively, the professional learning community members were able to solve the problem and, through knowledge building conversations, were able to strengthen their own mathematical understandings. Non-routine, complex problems helped the learning community to create and use mathematical spaces for discovery, collaboration, and broader knowledge building conversations. Technologically, we learned to capitalize on a technological affordance, which gave us the ability to draw lines with ease. Participants in the learning community also learned how to establish an identity by choosing unique colours for the drawing tools. Problems that required colored lines to demonstrate a mathematical solution resulted in an explosion of participant engagement and interactive drawing on the whiteboard. Participants engaged with each other and with the mathematical problems using the whiteboard tools, interactive chat, and audio tools. Non-routine, complex problems that connected mathematical ideas and also required minimal drawing on the whiteboard were excellent problems for encouraging online, collaborative, and engaging problem solving.
Through this hermeneutics study, it was determined that with the right conditions, collaborative mathematical problem solving is not only possible in the synchronous online environment, it can lead to collective knowledge building for learning and teaching with mathematics. Finding non-routine, discrete mathematics problems facilitated the participants’ engagement and mathematical discovery as learners, and fostered conversations about fostering this kind of learning for the teachers’ own learners in the classroom. Adapting the mathematical problems to minimize writing and emphasizing drawing was observed to facilitate increased whiteboard interaction and participant contributions to mathematical conversations. Giving the community time to adapt and learn how to use the Elluminate interface is also essential. Based on our experiences, the online synchronous environment provided opportunities for geographically dispersed individuals to collectively learn about collaborative mathematical problem solving in an online professional learning community.
This paper contributes to the literature in open and distance learning by linking research and practice to gain insights into the experiences of participants in the online learning environment. With the proliferation of oTPD in a number of content areas, little is known about the actual social and cognitive processes in which its participants engage during those experiences, nor has enough been said about the limitations imposed by online spaces and tools. This article investigates these processes and should be of interest to researchers, administrators, teachers, and instructional designers.
The following recommendations for the design and support of online teacher professional development for mathematics inquiry emerged from this study. Plan for the first session to serve as an introduction to each other, to collaborative mathematical problem solving, and to the technology. Have a good mathematics problem selected, but expect mathematics to be in the background at first as participants become familiar and fluent with the interactive online environment. Give participants opportunities to play with the whiteboard tools to familiarize themselves with the affordances and constraints of the online environment. Establish protocols for identifying each other and having a distinct presence on the whiteboard. For instance, have each participant choose a unique colour and develop an identity colour code. Bring mathematical and teaching experts together to help facilitate conversations and keep content relevant to the discipline of mathematics. Choose complex non-routine mathematical problems where solution methods can be found with easily drawn symbols and lines. Be responsive to the group finding and contributing mathematical problems that are relevant and interesting. Allow sufficient time to establish a community to facilitate meaningful conversations and learning.
Before embarking on an online professional development program, online professional developers need to anticipate technological challenges and rely on the first session to trouble shoot, to diagnose connection and interaction affordances and constraints, and to introduce and orient the participants to the learning topics as well as the online learning environment for interaction and collaboration with mathematics and with each other. Learning leaders need to have a good mathematical problem or two ready for the first session; however, hold off on the enthusiasm for mathematical problem solving until technical issues are taken care of and the participants gain fluency in navigating the online learning space. Plan time for the participants to play with the technology. Hold pre-sessions to test the problems in the environment before every session. Trouble shooting and problem solving in pre-sessions informed and enhanced each session. The disciplinary expertise of the mathematician and the mathematics educator were invaluable to the emergent learning design process. The shared understandings and deeply held expertise shaped the participants’ learning, the online mathematician’s learning, and the researchers’ learning. Problems that required line drawings for solutions worked the best in this design. Lastly, find complex problems that draw upon multiple mathematical concepts. Adapt these problems to suit the online environment and encourage interaction on the whiteboard.
Future research should follow up with the participants to investigate whether the professional learning transferred to the classroom. If so, what transferred and how? Continued research is needed to understand what knowledge is needed for teaching mathematics, how that knowledge can be incorporated in the classroom, and how online teacher professional learning can inform new understandings and change mathematics teaching. Such research should be contextual with research and practice informing mathematics teaching in a cyclical process that builds understanding and capacity.
Alberta Education. (2012). Technology in schools: Alberta Supernet. Retrieved from http://education.alberta.ca/admin/technology/supernet.aspx
Alberta Education. (2007). Mathematics: Kindergarten to grade 9. Alberta Government. Retrieved from http://www.education.gov.ab.ca/k%5F12/curriculum/bySubject/math/Kto9Math.pdf
Ball, D. L., Thames, M. H., & Phelps, G. (2008). Content knowledge for teaching: What makes it special? Journal of Teacher Education, 59(5), 389–407.
Borko, H. (2004). Professional development and teacher learning: Mapping the terrain. Educational Researcher, 33(8), 3–15. doi:10.3102/0013189X033008003
Clifford, P., & Friesen, S. (2003). Hard fun: Teaching and learning for the 21st century. In Back to the basics: “Thinking the world together”. Mahwah, NJ: Lawrence Erlbaum Associates, Inc.
Clifford, P., Friesen, S., & Lock, J. (2004). Coming to teaching in the 21st century: A research study. Retrieved from http://www.galileo.org/research/publications/ctt.pdf
Darling-Hammond, L., & Bransford, J. (2007). Preparing teachers for a changing world: What teachers should learn and be able to do. John Wiley & Sons.
Darling-Hammond, L., & McLaughlin, M. W. (2011). Policies that support professional development in an era of reform. Phi Delta Kappan, 92(6), 81–92.
DeBellis, V. A., & Rosenstein, J. G. (2004). Discrete mathematics in primary and secondary schools in the United States. ZDM, 36(2), 46–55. doi:10.1007/BF02655758
Dede, C. (2004a). Enabling distributed learning communities via emerging technologies--Part One. T.H.E. Journal, 32(2). Retrieved from http://ezproxy.lib.ucalgary.ca:2048/login?url=http://search.ebscohost.com/login.aspx?direct=true&db=eric&AN=EJ709366&site=ehost-live
Dede, C. (2004b). Enabling distributed learning communities via emerging technologies--Part Two. T.H.E. Journal, 32(3). Retrieved from http://ezproxy.lib.ucalgary.ca:2048/login?url=http://search.ebscohost.com/login.aspx?direct=true&db=eric&AN=EJ709427&site=ehost-live
Dede, C., Ketelhut, D. J., Whitehouse, P., Breit, L., & McCloskey, E. M. (2009). A research agenda for online teacher professional development. Journal of Teacher Education, 60(1), 8–19.
DuFour, R., DuFour, R., Eaker, R., & Many, T. W. (2010). Learning by doing: A handbook for professional learning communities at work (2nd ed.). Bloomington, IN: Solution Tree Press. Retrieved from http://www.solution-tree.com/learning-by-doing.html
Fernandez, C., & Yoshida, M. (2004). Lesson study: A Japanese approach to improving mathematics teaching and learning. Mahwah, NJ: Lawrence Erlbaum.
Flyvbjerg, B. (2001). The power of example. In Making social science matter (pp. 66–87). Cambridge, UK: University Press.
Friesen, N. (2009). Chapter six: Hermeneutic phenomenology: Experiential evidence in e-learning. In Re-thinking e-learning research (pp. 119–148). New York, NY: Peter Lang Publishing.
Friesen, S. (2008). Math: Teaching it better. In Back to the basics (Vol. 2, pp. 135–141). New York, NY: Routledge.
Gadamer, H.-G. (1989). Truth and method. (J. Weinsheimer & D. G. Marshall, Trans.) (2nd ed.). New York: Continuum Press.
Glazer, E. M., Hannafin, M. J., Polly, D., & Rich, P. (2009). Factors and interactions influencing technology integration during situated professional development in an elementary school. Computers in the Schools, 26(1), 21. doi:10.1080/07380560802688257
Goldin, G. A. (2010). Problem solving heuristics, affect, and discrete mathematics: A representational discussion. In B. Sriraman & L. D. English (Eds.), Theories of mathematics education: Seeking new frontiers (pp. 241–250). Heidelberg: Springer-Verlag. DOI: 10.1007/978-3-642-00742-24.
Heidegger, M. (1962). Being in time. New York, NY: HarperSanFrancisco.
Heidegger, M. (1977). The question concerning technology. In The question concerning technology and other essays (pp. 3–35). New York: Harper & Row.
Hiltz, S. R. (1998). Collaborative learning in asynchronous learning networks: Building learning communities. Retrieved from http://www.eric.ed.gov/ERICWebPortal/detail?accno=ED427705
Jacobs, J. K., Hiebert, J., Givvin, K. B., Hollingsworth, H., Garnier, H., & Wearne, D. (2006). Does eighth-grade mathematics teaching in the United States align with the NCTM “standards?” Results from the TIMSS 1995 and 1999 video studies. Journal for Research in Mathematics Education, 37(1), 5–32.
Jacobsen, D. M. (2006). Learning technology in continuing professional development: The Galileo Educational Network. New York, NY: Edwin Mellen Press.
Jardine, D. W. (2006). Chapter 10: “The fecundity of the individual case”; Considerations of the pedagogic heart of interpretive work. In Curriculum in abundance (pp. 151–168). Mahwah, NJ: Lawrence Erlbaum.
Jonassen, D. H. (2004). Learning to solve problems: An instructional design guide. San Francisco, CA: John Wiley & Sons.
Jones, T., & Cuthrell, K. (2011). YouTube: Educational potentials and pitfalls. Computers in the Schools, 28(1), 75. doi:10.1080/07380569.2011.553149
Kaplan, R., & Kaplan, E. (2007). Out of the labyrinth: Setting mathematics free. New York, NY: Oxford University Press.
Lewis, T. (2002). The math fair booklet. Vancouver, BC: The Pacific Institute of Mathematics.
Lieberman, A., & Grolnick, M. (2005). Educational reform networks: Changes in the forms of reform. In M. Fullan (Ed.), Fundamental change (pp. 40–59). Springer Netherlands. Retrieved from http://www.springerlink.com.ezproxy.lib.ucalgary.ca/content/k1256241p8786274/abstract/
Mackey, J., & Evans, T. (2011). Interconnecting networks of practice for professional learning. The International Review of Research in Open and Distance Learning, 12(3), 1–18.
Marrero, M. E., Woodruff, K. A., Schuster, G. S., & Riccio, J. F. (2010). Live, online short-courses: A case study of innovative teacher professional development. International Review of Research in Open and Distance Learning, 11(1), 81–95.
Martin, M. O., Mullis, I. V. S., & Foy, P. (2008). TIMSS 2007 international science report: Findings from IEA’s trends in international mathematics and science study at the fourth and eighth grades.
Moore, M. G. (1989). Three types of interaction. American Journal of Distance Education, 3(2), 1–6.
Moore, M. G. (2007). A theory of transactional distance. In M. G. Moore (Ed.), Handbook of distance education (Vol. 2, pp. 89–108). Mahwah, NJ: Lawrence Erlbaum.
Moore, M. G. (1993). Theory of transactional distance. In Theoretical principles of distance education (pp. 22–38). London: Rutledge.
Mullis, I. V. S., Martin, M. O., Gonzales, E. J., & Chrostowski, S. J. (2004). TIMSS 2003 international mathematics report. Chestnut Hill, MA: IEA. Retrieved from http://timss.bc.edu/timss2003i/mathD.html
Plante, J., & Beattie, D. (2004). Connectivity and ICT integration in Canadian elementary and secondary schools: First results from the Information and Communications Technologies in Schools Survey, 2003-2004. Ottawa, ON: Statistics Canada. Retrieved from http://www.statcan.gc.ca/pub/81-595-m/81-595-m2004017-eng.pdf/
Preciado-Babb, A. P., & Liljedahl, P. (2012). Three cases of teachers’ collaborative design: Perspectives from those involved. Canadian Journal of Science, Mathematics and Technology Education, 12(1), 22–35. doi:10.1080/14926156.2012.649052
Renninger, K. A., & Shumar, W. (2002). Building virtual communities: Learning and change in cyberspace. Cambridge University Press.
Rovai, A. P. (2002). Sense of community, perceived cognitive learning, and persistence in asynchronous learning networks. The Internet and Higher Education, 5(4), 319–332. doi:10.1016/S1096-7516(02)00130-6
Schoendfeld, A. H. (2009). Why do we teach? Kappa Delta Pi Record, 46(1), 26–29.
Smith, D. G. (1999). The hermeneutic imagination and the pedagogic text. In Pedagon (pp. 27–44). New York, NY: Peter Lang.
Statistics Canada. (2010, May 10). Internet use by individuals, by location of access, by province. Retrieved from http://www.statcan.gc.ca/tables-tableaux/sum-som/l01/cst01/comm36a-eng.htm
Stigler, J. W., & Hiebert, J. (1999). The teaching gap: Best ideas from the world’s teachers for improving education in the classroom. New York: Free Press.
Stigler, J. W., & Hiebert, J. (2009). The teaching gap: Best ideas from the world’s teachers for improving education in the classroom. New York, NY: First Free Press. (Original work published 1999).
Stoll, L., & Louis, K. S. (Eds.). (2007). Professional learning communities: Divergence, depth and dilemmas. McGraw-Hill International.
Trust, T. (2012). Professional learning networks designed for teacher learning. Journal of Digital Learning in Teacher Education, 28(4), 133–138.
Van Manen, M. (1997). Researching lived experience: Human science for an action sensitive pedagogy (Vol. 2). London, Ont.: Althouse Press.
Wenger, E., Trayner, B., & De Laat, M. (2011). Promoting and assessing value creation in communities and networks: A conceptual framework (No. 18). Open Universiteit, Ruud de Moor Centrum. Retrieved from http://isites.harvard.edu/fs/docs/icb.topic1116077.files/Assessing%20Learning%20Communities.pdf
1 Lily and Sharon chose to use their first names. All other participant names are pseudonyms.